 幾何学
幾何学 弧の求め方 – 数学の理解を深めよう!
数学での「弧」とは、円周の一部を指します。弧の長さを求めるには、いくつかの要素を知っておく必要があります。ここでは、弧の求め方に関する公式や例について詳しく解説していきます。 弧の長さの公式 弧の長さ \( L \) を求めるための基本的な...
 幾何学
幾何学  幾何学
幾何学  幾何学
幾何学  幾何学
幾何学  幾何学
幾何学  幾何学
幾何学  幾何学
幾何学 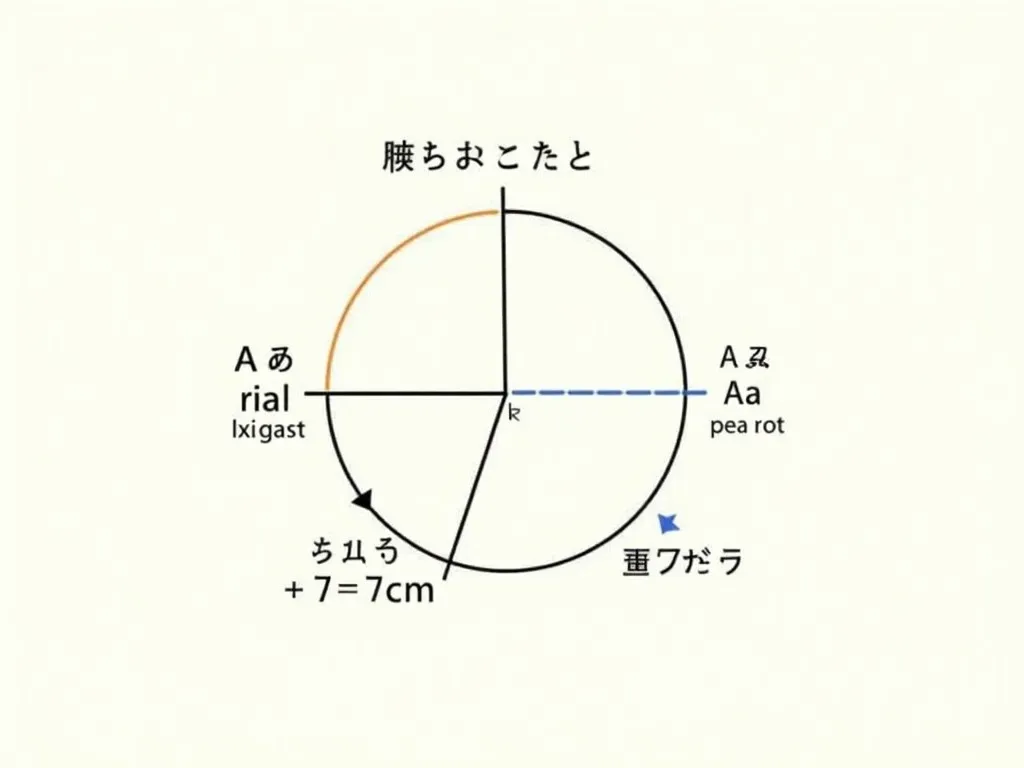 幾何学
幾何学  幾何学
幾何学  幾何学
幾何学