底面積とは、立体の底面の面積のことです。物体の形状によって異なる求め方が存在します。このページでは、さまざまな立体の底面積の求め方を探求します。🎓✨
1. 立体の種類と求め方
底面積は、主に以下の形状に分かれます:
- 立方体
- 直方体
- 円柱
- 円錐
- 三角柱
- 四角柱
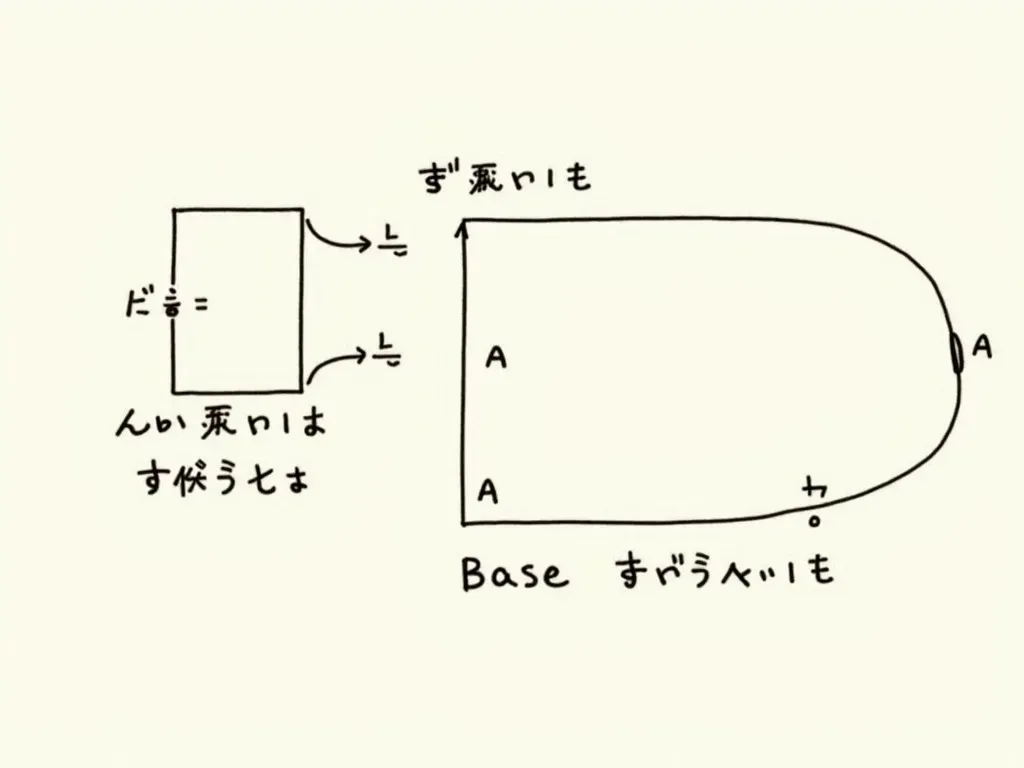
2. 立方体と直方体の底面積
立方体の底面積は、1つの辺の長さをaとした場合、次のように計算されます:
底面積 = a × a = a²直方体の場合、底面の縦の長さをl、横の長さをwとすると、次の公式が使えます:
底面積 = l × w3. 円柱の底面積
円柱の底面積は、半径をrとすると、以下のように表されます:
底面積 = π × r²こちらが円柱のモデルです。👇
4. 円錐の底面積
円錐の底面積も円柱と同じく、半径rを用いて以下のように求めます:
底面積 = π × r²5. 三角柱の底面積
三角柱では、底面が直角三角形である場合、底面積を求める公式は次の通りです。
底面積 = (1/2) × 底辺 × 高さ「数学の公式は、ピタゴラスの定理とともに、三角形の特性を理解する鍵です。」🗝️
6. 実践例
例えば、半径が3cmの円柱の底面積を求めると、次のようになります:
底面積 = π × 3² = 9π ≈ 28.27 cm²7. まとめ
底面積を求めることは、さまざまな立体の特性を理解するために重要です。🧮 計算が簡単な公式を使用することで、誰でも簡単に求めることができます。重要な点は、立体ごとの形状に適した公式を選択することです。
8. 参考資料
以下のリンクから、さらに詳しい内容をご覧いただけます: