ばね定数の求め方

ばね定数とは？

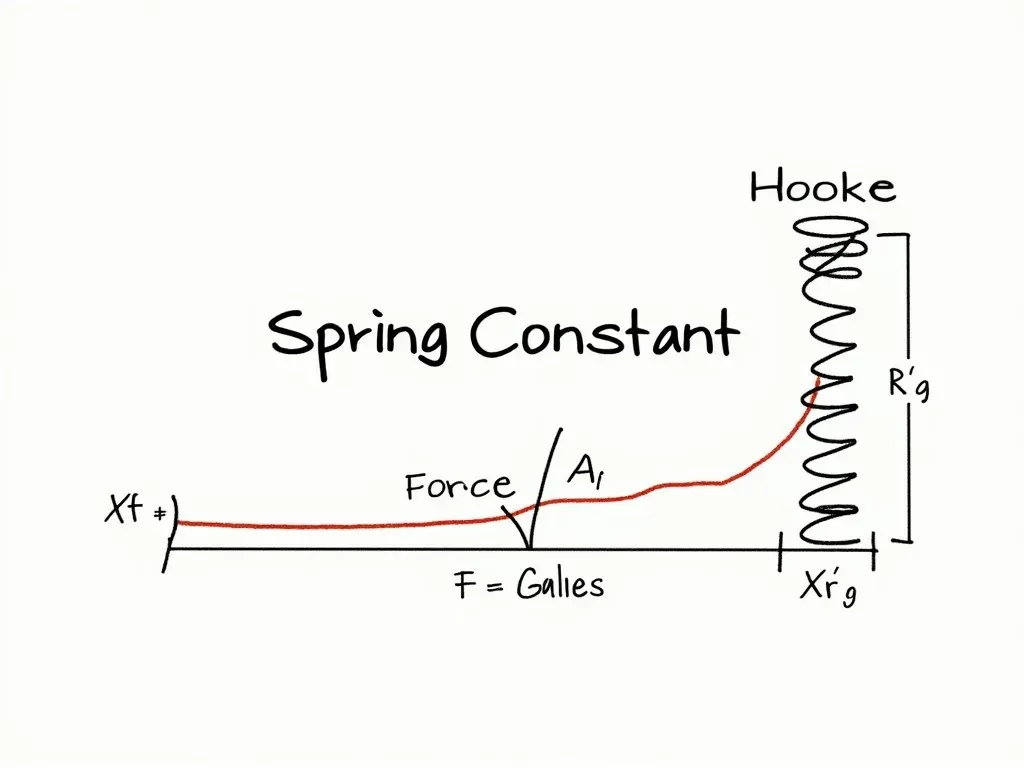
ばね定数（k）とは、ばねに加えた荷重Fとばねの伸びxとの関係を示す比例定数です。フックの法則により、次のように表されます：

$$ F = kx $$

ここで、力Fはニュートン（N）、ばね定数kはN/m（ニュートン毎メートル）で表され、~~思ったよりも難しくありません！~~ 簡単に計算できます。😊

ばね定数を求めるには、まず実験によって力と伸びの値を取得する必要があります。次に、以下の公式を使用します：

$$ k = \frac{F}{x} $$

たとえば、100Nの力で1.5cm（0.015m）伸びるばねがあるとします。この場合、ばね定数は次のように計算できます：

$$ k = \frac{100}{0.015} = 6666.67 \, \text{N/m} $$

ばねを直列または並列に接続すると、全体のばね定数が変化します。💡

直列接続の場合、全体のばね定数は次の式で求められます：

$$ \frac{1}{K} = \frac{1}{k_1} + \frac{1}{k_2} $$

たとえば、ばね定数がそれぞれk_1 = 100 \, \text{N/m}およびk_2 = 200 \, \text{N/m}の場合：

$$ \frac{1}{K} = \frac{1}{100} + \frac{1}{200} = \frac{3}{200} $$

よって、全体のばね定数は

$$ K = \frac{200}{3} \approx 66.67 \, \text{N/m} $$

並列接続の場合の式はシンプルです：

$$ K = k_1 + k_2 $$

したがって、同様のばね定数がk_1 = 100 \, \text{N/m}、k_2 = 200 \, \text{N/m}であれば：

$$ K = 100 + 200 = 300 \, \text{N/m} $$

次に、実際の問題を見てみましょう。

例えば、ある材料に力を加えたときに伸びが3cmだったとします。もしその力が150Nであれば、ばね定数は次のように求められます：

$$ k = \frac{150\, \text{N}}{0.03\, \text{m}} = 5000\, \text{N/m} $$

ばね定数は、力学や工学の基本的な要素であり、さまざまな分野で重要な役割を果たしています。求め方をマスターすることで、より複雑なシステムの解析が可能になります！

「曖昧さを取り除き、物理学を学ぶことは未来への第一歩です！」