直線の傾きは、その直線がどれだけ急であるかを示す重要な数値です。ここでは、直線の傾きを求めるための方法やその意義について詳しく解説します! 😊
1. 傾きの定義
直線の傾きは、垂直の移動距離(Δy)を水平の移動距離(Δx)で割ったものです。これを数式で表すと以下のようになります:
$$m = \frac{Δy}{Δx}$$
この数式から、傾き m が正の値であれば、直線は右上がり、負の値であれば右下がりであることがわかります。
2. 傾きを求めるステップ
ステップ1: 2つの点を決める
直線が通る2点 (x₁, y₁) と (x₂, y₂) を考えます。
ステップ2: 増分を計算する
増分を求める:
- Δy = y₂ – y₁
- Δx = x₂ – x₁
ステップ3: 傾きを計算する
上記の増分を用いて、以下のように傾きを計算します:
$$m = \frac{y₂ – y₁}{x₂ – x₁}$$
3. 例題とグラフ
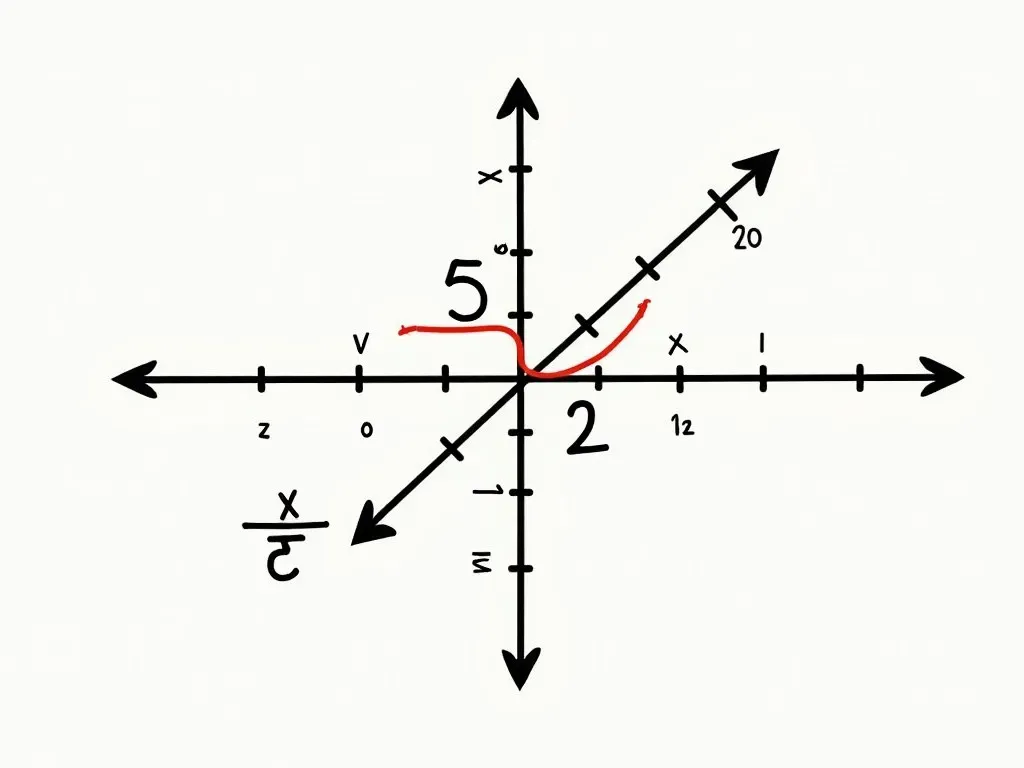
例えば、点 A (1, 2) と点 B (4, 5) の場合、傾きを求めてみましょう。
Δy = 5 – 2 = 3、Δx = 4 – 1 = 3 となりますので、傾きは:
$$m = \frac{3}{3} = 1$$
これは、直線が45度の角度で上昇していることを意味します。以下のグラフで確認してみましょう!
4. 傾きの直感的理解
直線の傾きが大きいほど、直線は急になります。傾きが0の場合は水平な直線を示し、傾きが無限大の場合は垂直な直線を示します。
考えてみてください;傾きが0の直線は“静止”しているかのようです。🚶♂️
5. 傾きを使った応用例
傾きは数学以上のものであり、物理など多くの分野で応用されています。例えば、速度の求め方、経済学における需要の変化など、さまざまな場面で役立ちます。
まとめ
直線の傾きを求める方法は、直感的であり、実用的です。数式の理解を深め、実際の問題に応用できるようになりましょう!📚✨