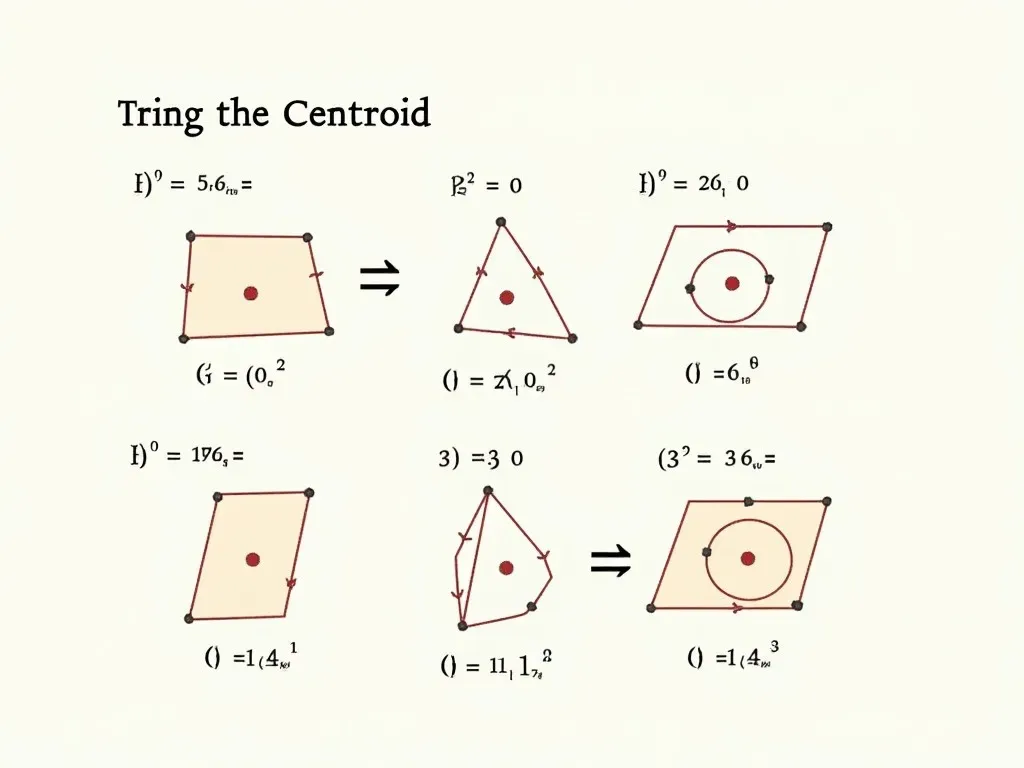
重心とは物体の重さが作用する点であり、力のモーメントを考慮して求めることができます。この記事では、重心の求め方について詳しく解説していきます。
重心の基本概念
重心は、物体を質量の点として考えたとき、その質量の合力が働く点です。具体的には、重さを考慮した中心と言えるでしょう。重心の求め方には様々な方法がありますが、主に次の3つのアプローチが一般的です:
- 座標を使った方法
- モーメントを用いた方法
- 面積比を使った方法
1. 座標を使った重心の求め方
座標を使用して重心を求める場合、各質点の座標と質量を考え、次の式を用います:
G_x = \frac{m_1 x_1 + m_2 x_2 + ... + m_n x_n}{m_1 + m_2 + ... + m_n}
G_y = \frac{m_1 y_1 + m_2 y_2 + ... + m_n y_n}{m_1 + m_2 + ... + m_n}
ここで、\(G_x, G_y\) は重心の座標、\(m\)は質点の質量、\(x, y\)はそれぞれの質点の位置座標です。
2. モーメントを用いた重心の求め方
モーメントの釣り合いを考えることで、重心を求めることも可能です。モーメントとは、力と力点との距離の積です。重心に関するモーメントの釣り合いは次のように表されます:
\sum M = 0
「モーメントに関する基本的な常識です。モーメントが釣り合っている点が重心です。」
3. 面積比を使った重心の求め方
図形の重心を求める際、面積比を使うことも効果的です。特に、三角形や四角形の場合には、各辺の比率に基づいて重心を簡単に特定できます。例えば、三角形の重心は、三角形のそれぞれの辺を2対1の比率で分ける点となります。
実例: 半円の重心
では、半径が 1 の半円の重心を求めてみましょう。この場合、重心の位置は一般的に次のように与えられます:
G = \left(0, \frac{4R}{3\pi}\right)
よって、半円の重心は \(y\) 軸上に位置し、具体的には高さが \(\frac{4R}{3\pi}\) です。
重心の応用
重心の概念は、物理学だけでなく様々な分野で重要です。例えば、建築物の安定性や、自動車のデザインなどにも影響を与えます。重心をうまく利用することで、より効率的な設計が可能となります。これを念頭に置いて、様々な状況での重心を考えてみてください!
「重心の理解は、力学や応用物理学の基本です。」
まとめ
重心は物体を支える基盤であり、モーメントや座標を使用して求めることができます。重心を知ることで、より深く物理や数学の世界を理解できるでしょう。ぜひ、実際の問題に適用してみてください!