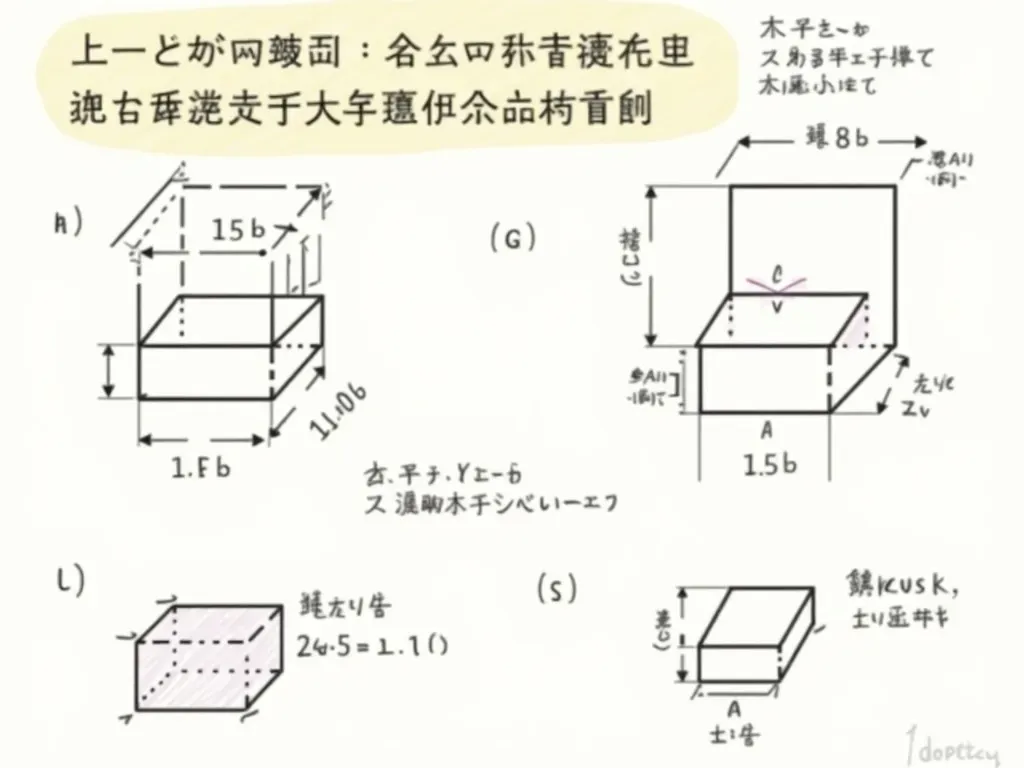
数学で学ぶ「角柱の体積」は、底面積と高さを用いて計算します。この記事では、具体例を使いながら、体積の求め方を詳しく解説します。 📐✨
1. 角柱の基礎概念
角柱は二つの合同な多角形の底面を持ち、それらを垂直に繋ぐ側面を持つ立体です。基本的には次の公式を使います:
\( V = S \times h \)
ここで、\( V \) = 体積, \( S \) = 底面積, \( h \) = 高さです。
2. 底面積の計算方法
底面の形が異なる角柱の場合、それぞれの面積を計算する必要があります。例えば:
- 三角柱: 底面が三角形の場合、\( S = \frac{1}{2} \times \text{底辺} \times \text{高さ} \)
- 四角柱: 底面が四角形の場合、\( S = \text{一辺} \times \text{一辺} \)
- その他の多角形: それぞれの面積を求める公式を用います。
3. 体積の計算例
例として、底面が三角形で高さが5cmの角柱を考えましょう。
底面の三角形の底辺が4cm、高さが3cmなら、底面積は:
\( S = \frac{1}{2} \times 4 \times 3 = 6 \, cm^2 \)
この場合、体積は:
\( V = S \times h = 6 \times 5 = 30 \, cm^3 \)
正確な単位を書くことをお忘れなく!📝
4. 視覚的理解のためのグラフ
まとめ
角柱の体積は非常にシンプルですが、基礎を理解することが重要です。 🧠📏
重要なポイントは、
- 底面積を正しく計算すること
- 高さを正確に測ること
- 単位に注意すること
知識を深めるために、例題を解いてみることをお勧めします! 💪