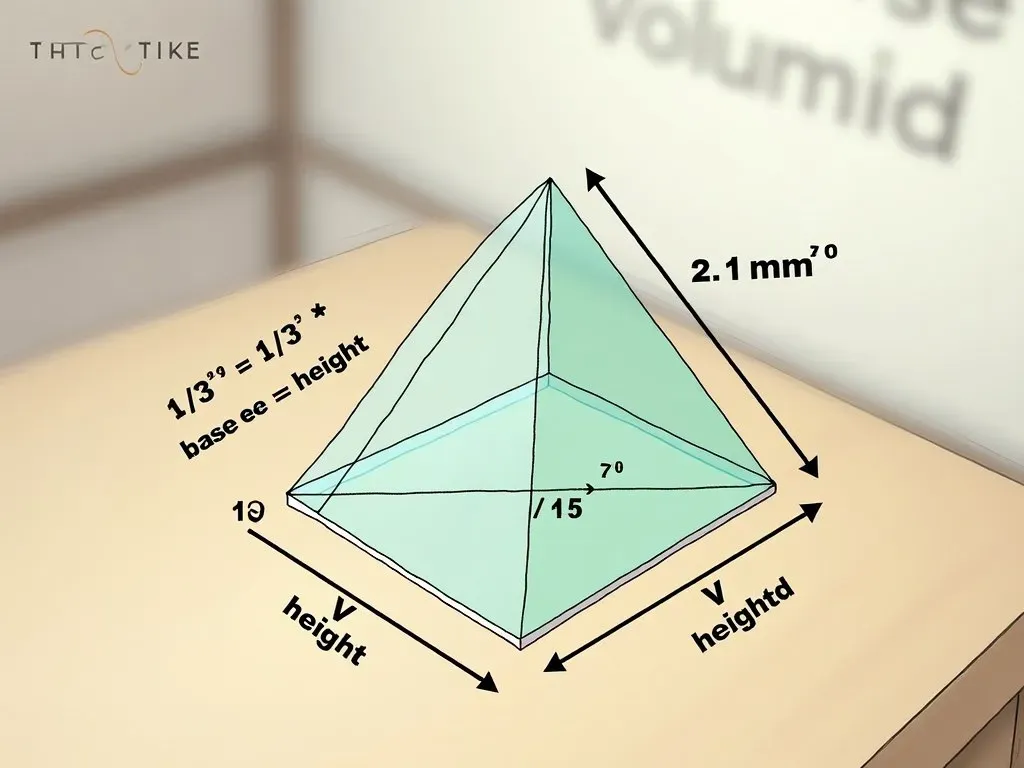
四角錐の体積を求める公式は非常にシンプルで、以下の数式で表されます:
\[\text{体積} = \frac{1}{3} \times \text{底面積} \times \text{高さ}\]
基本的な公式の確認
ここでの「底面積」は四角錐の底面の面積を指し、例えば、正方形の場合は以下のように計算します:
\[\text{底面積} = a^2\] (ここで \( a \) は底面の一辺の長さ)
具体例を見てみましょう
例えば、底面の一辺の長さが \( a = 4 \) cm 、高さが \( h = 6 \) cm の四角錐を考えます。
この場合、底面積は:
\[\text{底面積} = 4^2 = 16 \text{ cm}^2\]
したがって、体積は:
\[\text{体積} = \frac{1}{3} \times 16 \times 6 = 32 \text{ cm}^3\]
可視化で理解を深める
以下のグラフは、異なる底面の一辺の長さと高さに応じて四角錐の体積がどのように変化するかを示しています。
まとめ
「四角錐の体積を求めるのは簡単ですが、正確な計算が必要です!」📝
このガイドを参考にして、四角錐の体積を求める方法をマスターしてください!
詳細な公式や例題については、他の専門サイトも参考にするとより理解が深まります。
参考リンク: