円の中心を知っていることは、幾何学の基本的な問題を解く上で非常に重要です。円の中心を求める方法は、実際にはいくつかの方法があります。このページでは、様々な方法とその理論的な背景について詳しく解説していきます。
1. 円の定義と中心の概念
円は、平面上の点の集合であり、ある一定の距離(半径)から成る中心点によって、円周を形成します。したがって、円の中心は円周上の任意の点から同じ距離にある特別な点です。🌀
2. 円の中心を求める方法
円の中心を求める方法はいくつか紹介します。
2.1 垂直二等分線を使う方法
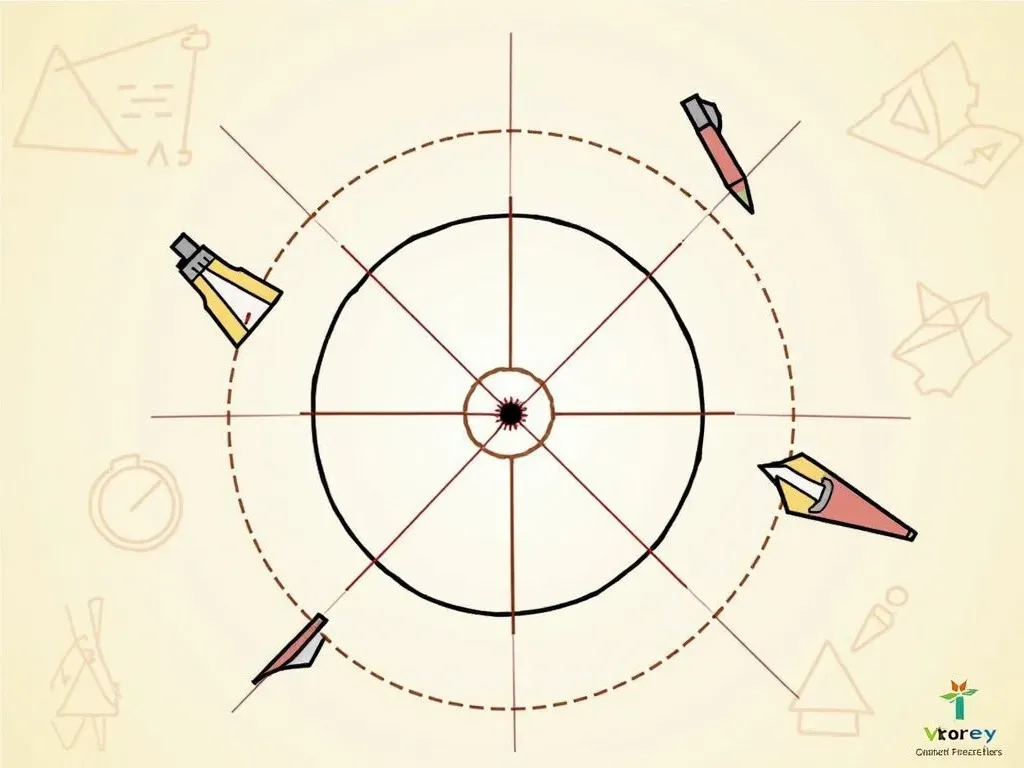
この方法では、円周上の2つの点を選び、その中点を結びます。この直線の垂直な線を描くと、円の中心に到達することができます。✏️
まず、円周上の2点AとBを選び、その中点を求めます。この直線の垂直二等分線が中心を指し示します✨
2.2 コンパスを使う方法
コンパスを利用して、円周上の3点を選び、その各辺に対して円を描画します。これらの円の交点が円の中心となります。🔍
2.3 数式を使って求める方法
円の一般形の方程式は、x^2 + y^2 + Dx + Ey + F = 0のように表せます。ここから中心の座標を求めるには、次の式を使用します:
中心の座標 = \left(-\frac{D}{2}, -\frac{E}{2}\right)
3. 図を用いた説明
次に、円の中心を求めるための図を用いて、理解を深めましょう。
4. まとめ
円の中心を求めることは、非常に重要なわけですが、その求め方には様々なアプローチが存在します。それぞれの方法には、特定の文脈や状況での利点があります。これにより、円の幾何学的特性を理解しやすくなります。🎉
皆さんも、ぜひこの方法を実践してみてください!質問や疑問があれば、コメント欄にお気軽にどうぞ!