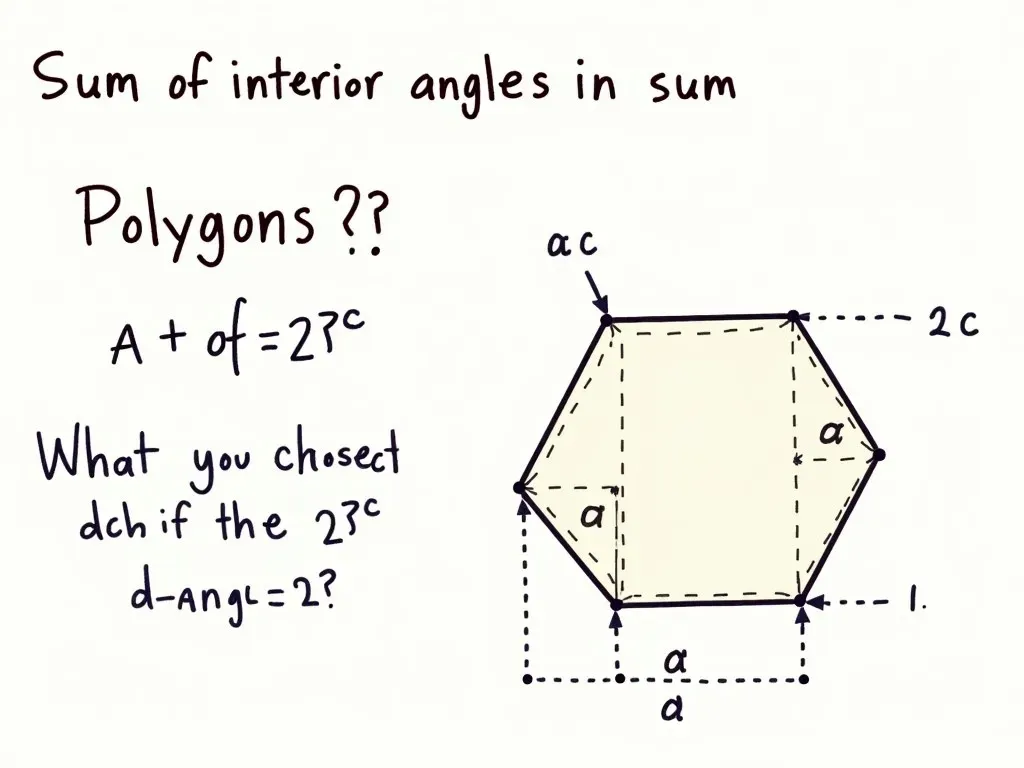
多角形の内角の和を求める公式は非常に重要です。この公式を使えば、さまざまな多角形の内角の和を簡単に計算できます。内角の和は、次のように表されます:
内角の和 = \(180^\circ \times (n – 2)\)
ここで、\(n\)は多角形の辺の数です。例えば、三角形(3角形)の内角の和は、
\[ 180^\circ \times (3 – 2) = 180^\circ \]
四角形(4角形)の場合、
\[ 180^\circ \times (4 – 2) = 360^\circ \]
公式の証明
この公式がなぜ成り立つのかを理解するために、いくつかの方法で証明を行います。
方法1: 三角形に分割する
多角形を三角形に分割することを考えます。例えば、五角形の場合、次のように三角形に分割できます:

この図では、頂点から対角線を引いて三角形に分割しています。
このように、\(n\)角形は\(n-2\)個の三角形に分割でき、それぞれの内角の和は180°です。
方法2: 外角の和を使う
全ての多角形の外角の和は360°です。内角と外角は以下のように関係しています:
\[ 内角 + 外角 = 180^\circ \]
この関係を利用すれば、内角の和も求めることができます。
方法3: 数学的帰納法
数学的帰納法を使って、この公式の正しさを証明することもできます。
まず、基本ケースとして、三角形(\(n=3\))の場合を確認します。次に、仮定として\(n=k\)の場合が成り立つとし、\(n=k+1\)の場合での成り立ちを示します。
例題
次の多角形の内角の和を求めてみましょう:
七角形の場合、\(n=7\)ですので、
\[ 180^\circ \times (7 – 2) = 900^\circ \]
これにより、七角形の内角の和は900°であることが分かります。
まとめ
いかがでしたでしょうか?内角の和の求め方は、公式を用いることで簡単に計算できることが分かりました。ぜひ、他の多角形の内角の和も試してみてください。