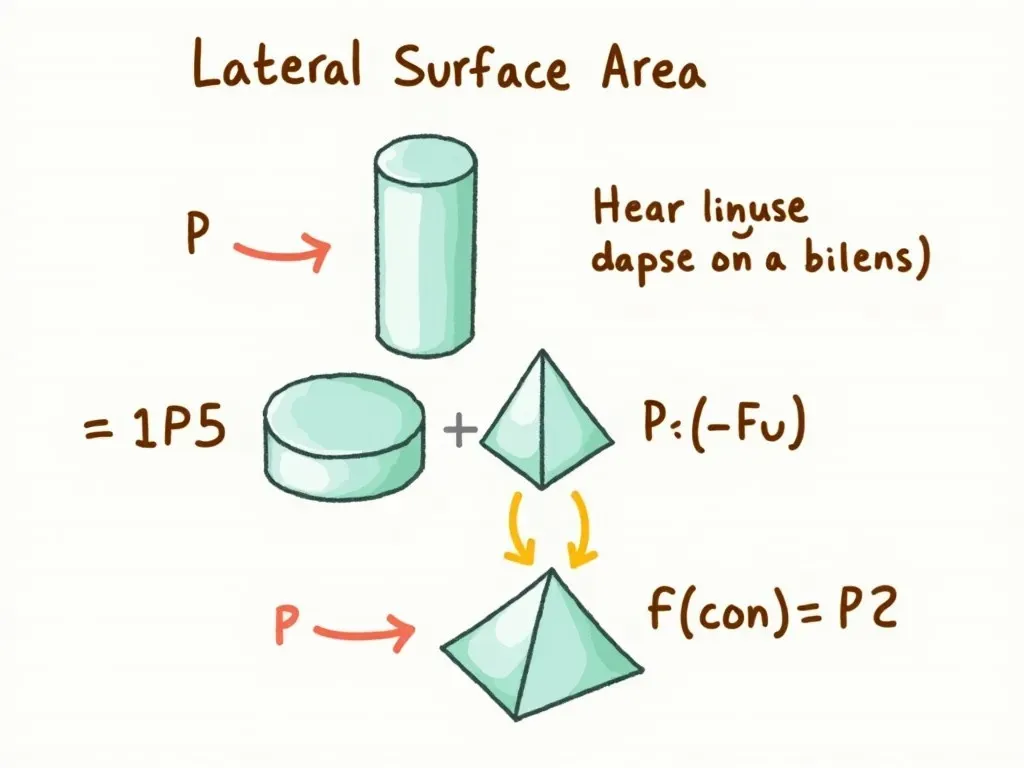
数学の中でも特に面積の計算は重要です。特に円錐や円柱といった三次元の形状においては、側面積を求めることが非常に重要です。このガイドでは、円錐と円柱の側面積を求める方法を解説します。
1. 円錐の側面積の求め方
円錐の側面積は、次の式を使って求めます:
\[ S = \pi r l \]
ここで、\( r \) は底面の半径、\( l \) は母線の長さです。この公式を用いて、実際に計算してみましょう!
例題
半径3cm、母線の長さ4cmの円錐の側面積を求めます。
まず、公式を使います:
S = π × 3 × 4 = 12π cm²したがって、側面積はおおよそ \( 37.68 cm² \) です。🎉
2. 円柱の側面積の求め方
円柱の側面積を求める公式は次の通りです:
\[ S = 2\pi rh \]
ここで、\( r \) は底面の半径、\( h \) は高さです。
例題
半径5cm、高さ10cmの円柱の側面積を求めます。
S = 2 × π × 5 × 10 = 100π cm²判明した側面積はおおよそ \( 314.16 cm² \) です。👍
3. 視覚的な理解を深めるためのグラフ
まとめ
今回は、円錐と円柱の側面積を求める方法を説明しました。数学は難しいと思うかもしれませんが、公式を使ったり例題を解いたりすることで、理解が深まります。さらに質問があれば、気軽に聞いてくださいね!