三角形高さの求め方 – 完全ガイド

三角形の高さの求め方はいくつかあり、三角形の種類や与えられるデータによって異なります。ここでは、主な方法について詳しく解説します。🎓✨

1. 三角形の基本性質

三角形の高さ（h）とは、底辺（b）から対角の頂点までの垂直な距離を指します。三角形の面積（A）は以下の式で求められます：

$$ A = \frac{1}{2} \times b \times h $$

2. 底辺と高さが分かっている場合

もし底辺の長さが分かっていれば、面積から高さを求めることができます。面積が既知である場合、以下のようになります：

$$ h = \frac{2A}{b} $$

3. 三辺の長さが分かっている場合 – ヘロンの公式

三角形の三辺の長さを a, b, c とすると、ヘロンの公式を使って面積 A を求めることができます。まず、半周長 s を求めます：

$$ s = \frac{a + b + c}{2} $$

面積は次のように計算されます：

$$ A = \sqrt{s(s – a)(s – b)(s – c)} $$

その後、高さは先程述べた公式を使用して求めます。

4. 正三角形の高さ

正三角形の高さは、1辺の長さ（l）が分かれば簡単に求められます：

$$ h = \frac{l \sqrt{3}}{2} $$

例えば、辺の長さが 6 の正三角形の場合、高さは：

$$ h = \frac{6 \sqrt{3}}{2} = 3 \sqrt{3} $$

5. 直角三角形の場合

直角三角形では、底辺（a）と他の直角の隣接辺（b）の長さが分かっている場合、ピタゴラスの定理を使って高さを求めることができます：

$$ c^2 = a^2 + b^2 $$

高さは直接利用できないですが、代入して求めることが可能です。

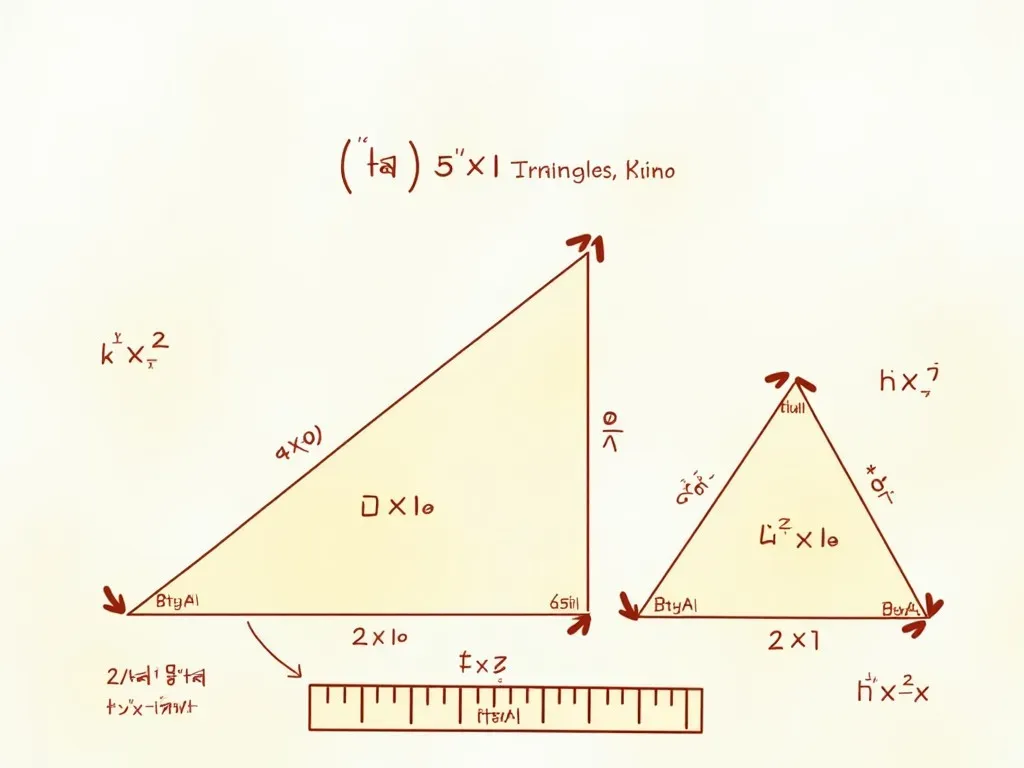
6. 絵で見る三角形の高さ

上のグラフは直角三角形を示しています。高いところから底辺までの距離が高さです。

7. まとめ

以上のように、三角形の高さの求め方はいろいろあります。適切な方法を選ぶことで、正確な計算が可能です。🔍📐

「数学は常に手を貸してくれる友です！」