三角形の重心(じゅうしん)とは、三角形の3つの辺の中点を結ぶ中線の交点であり、重要な数学の概念です。今回は、その求め方や性質について詳しく解説していきます!✨
重心の定義
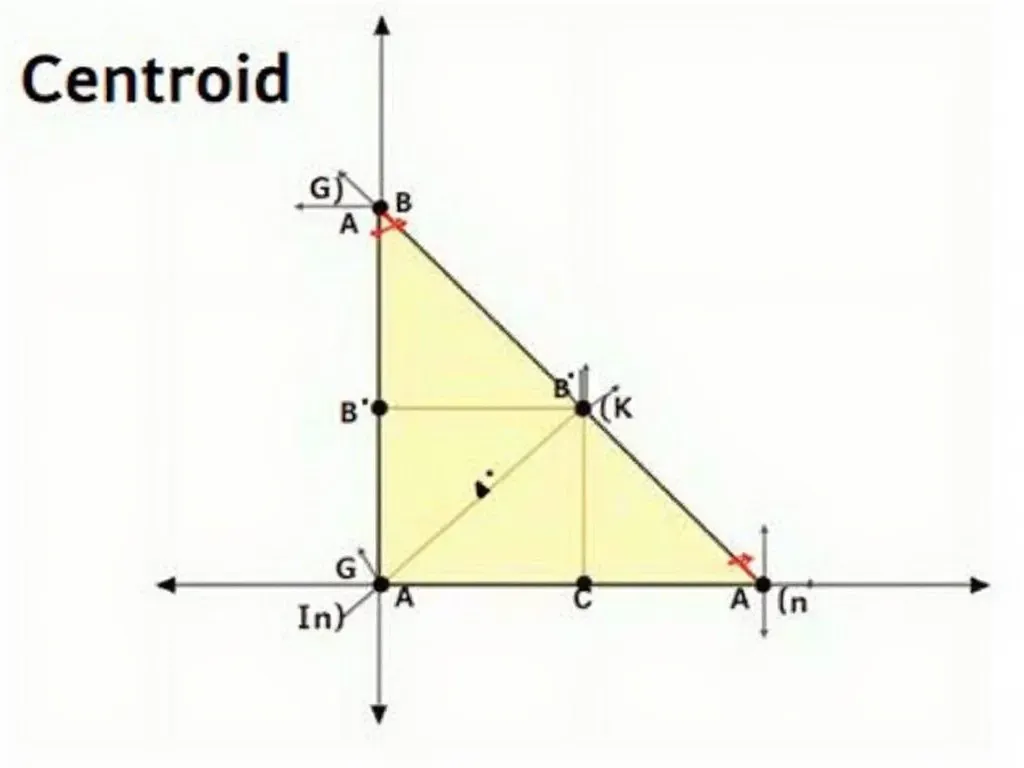
三角形の重心は、次のように定義されます。中線が交わる点であり、この点は各中線を2:1に内分します。これを視覚的に表現すると:
重心の求め方
三角形の重心を求めるための一般的な方法は、次の公式を使います。
G(x, y) = \left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right)
ここで、Gは重心、x_1, y_1, x_2, y_2, x_3, y_3は三角形の各頂点の座標です。重心は、各頂点の座標の平均値として計算されます。
具体例
次の三角形の重心を求めてみましょう。
- 頂点A(0, 0)
- 頂点B(2, 3)
- 頂点C(4, 0)
この場合、重心Gの座標は次のように計算できます:
G = \left( \frac{0 + 2 + 4}{3}, \frac{0 + 3 + 0}{3} \right) = \left( 2, 1 \right)
重心の性質
重心には以下のような性質があります。
重心は三角形の平衡点であり、物理的には重さの中心として理解されます。
中線の交点性
三角形の各中線は、重心で交わります。これは次のように示されます。
中線は、各頂点から対辺の中点に引かれた線です。中線を引くと、重心がどこにあるかが分かります。
まとめ
三角形の重心の求め方を学ぶことで、数学の理解が深まります。計算式や性質を使って、さまざまな問題に取り組んでみましょう!💡最後に、他の図形の重心や資源とも関連させて、より広い視点を持つことが大切です。
以上が「三角形の重心の求め方」に関する解説でした!楽しんで学びましょう!😊