こんにちは!今日は、ひし形の面積を求める方法について学びましょう。ひし形は四角形の一種で、全ての辺が同じ長さを持つ特別な形です。では、さっそく公式を見ていきましょう!📏✨
ひし形の面積を求める公式
ひし形の面積は、主に2つの方法で求められます。以下にその公式を示します。
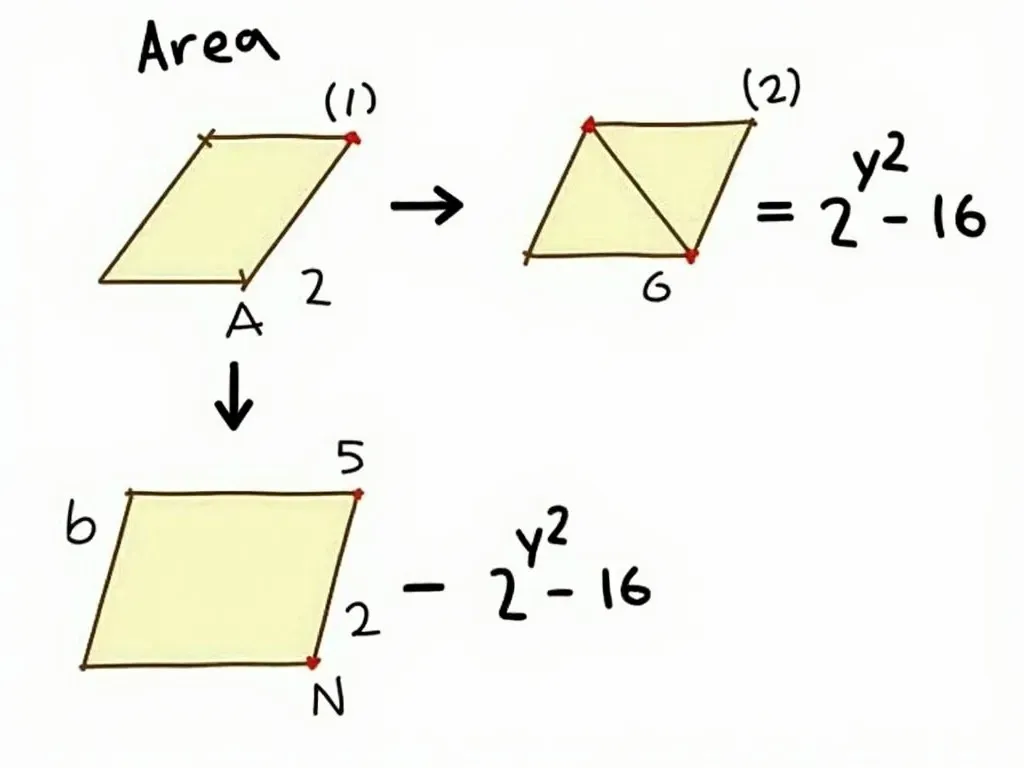
1. 対角線を使った方法
ひし形の面積は、対角線の長さを使って計算できます。公式は以下の通りです。
面積 \( A \) は、対角線 \( d_1 \) と \( d_2 \) を用いて次のように計算します:
\[ A = \frac{d_1 \times d_2}{2} \]
2. 高さと底辺を使った方法
もう一つの方法は、高さ \( h \) と底辺 \( a \) を使った計算です。
この場合の公式は次のようになります:
\[ A = a \times h \]
計算例
対角線を使った計算例
例えば、対角線の長さがそれぞれ \( d_1 = 8 \) cm と \( d_2 = 6 \) cm の場合、面積は次のように計算できます:
\[ A = \frac{8 \times 6}{2} = 24 \text{ cm}^2 \]
高さと底辺を使った計算例
また、底辺が \( a = 5 \) cm で、高さが \( h = 4 \) cm の場合、面積は:
\[ A = 5 \times 4 = 20 \text{ cm}^2 \]
面積の求め方の視覚化
次に、ひし形の面積の計算を視覚的に表現しましょう!以下のグラフは、異なる対角線の長さに応じた面積の変化を示しています。
重要なポイント
- ⏳ 公式を覚える際は、ひし形の特性を考慮しましょう。
- ✏️ 問題を解くときは、まず全ての情報を整理することが重要です。
- 💡 高さがわからない場合は、他の方法で求めることもできます!
まとめ
ひし形の面積を求める方法は非常にシンプルですが、公式の意味を理解することが重要です。対角線と高さのどちらでも計算できますので、状況に応じて適切な方法を選んでください!
さあ、次は自分で問題を作ってみてくださいね。🌟