台形面積求め方 – 詳しい解説と公式

台形の面積を簡単に求められる公式を解説します！😄

台形の定義

台形とは、少なくとも一組の対辺が平行な四角形のことです。具体的には、上底と下底の二つの辺が平行です。

台形の面積を求めるには、上底(b₁)、下底(b₂)、高さ(h)を使います。

すべての問題はシンプルな公式で解決できる！✨

台形の面積(A)は次の公式で求めることができます：

A = \(\frac{(b_1 + b_2) \cdot h}{2}\)

つまり、中間部分の距離（上底と下底の和）に高さをかけて、最終的に2で割ります。この公式を用いれば、誰でも台形の面積を計算できますよ！📏

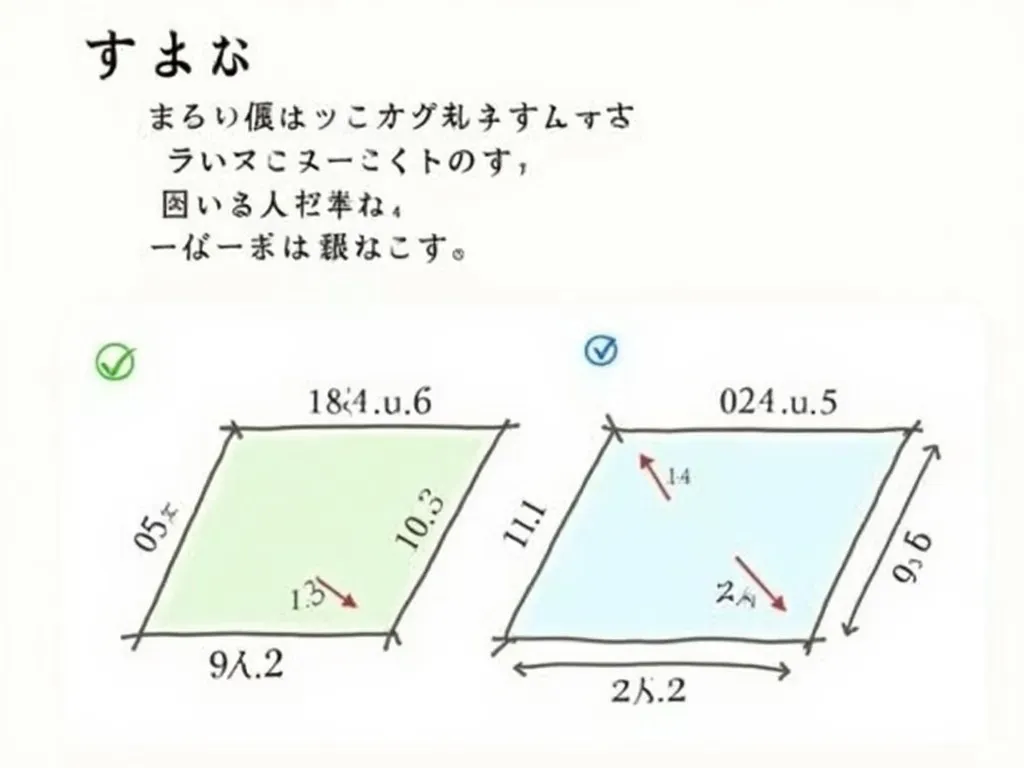
上底が5cm、下底が7cm、高さが4cmの台形の面積を求めます。

        A = \(\frac{(5 + 7) \cdot 4}{2}\)
        = \(\frac{12 \cdot 4}{2}\)
        = \(\frac{48}{2} = 24\) cm²

したがって、この台形の面積は24 cm²です。

上底が2.8cm、下底が3.7cm、高さが4.2cmの台形はどうでしょうか？

        A = \(\frac{(2.8 + 3.7) \cdot 4.2}{2}\)
        = \(\frac{6.5 \cdot 4.2}{2}\)
        = \(\frac{27.3}{2} = 13.65\) cm²

この台形の面積は13.65 cm²です！👏

台形の面積の概念を視覚的に理解するために、以下のグラフを使ってみましょう。